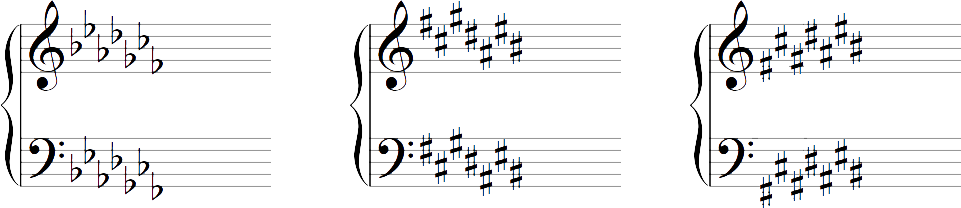Das Allerheiligste in der tonalen Musiktheorie: Die Quinte
Der Gral in der tonalen Musiktheorie ist also die allgegenwärtige Quinte.
Schauen wir uns noch ein paar Querverbindungen an.
Bei den Stammtönen wurde die Frage aufgeworfen, warum die eigentlich C-Dur-Tonleiter keine Vorzeichen hat, obwohl auch A- oder F-Dur durchaus Sinn ergeben hätten. Schauen wir uns nochmal die F-Dur-Variante an.
Das F als Startton der Stammtöne würde aus Quint-Sicht durchaus naheliegen. Beginnt man im Abstand der Quinten mit F, erhält man alle Stammtöne fein säuberlich bis zum B:
| F | C | G | D | A | E | B |
Wenn man diese Struktur zugrunde legt, finden sich alle Vorzeichen wie von selbst:
| F# | C# | G# | D# | A# | E# | B# | ||||||||||||||||
| F | C | G | D | A | E | B | | | F | C | G | D | A | E | B | | | F | C | G | D | A | E | B |
| F♭ | C♭ | G♭ | D♭ | A♭ | E♭ | B♭ |
Wenn man übrigens immer zwei Quinten als Pärchen betrachtet und oktaviert, erhält man alle Vorzeichen dicht zusammen innerhalb einer Oktave. Dies ist zum Beispiel auch bei den Vorzeichen teilweise ersichtlich. Während die ♭ fein säuberlich aufgereiht sind (links), verschleiern die # diese in der Standardanordnung (Mitte):
Hätte man mit dem ersten # (F#) unten angefangen (rechte Abbildung), wäre es auch hier sichtbar geworden. Vermutlich ist das F# auf der obersten Linie aber optisch viel auffälliger als jenes eine Oktaver tiefer. Wir wollen den (historisch erst nach den ♭ aufgetauchten) Kreuzen # diese kleine Unstimmigkeit aber gerne nachsehen.
Übrigens haben benachbarte Quinten immer die gleichen Vorzeichen (zwei # oder zwei ♭). Einzige Ausnahmen hiervon bilden nur die beiden Grenztöne F und B. Dort gibt es immer nur ein Vorzeichen.
Es ist schon ein wahres Mysterium, warum ausgerechnet die stets allgegenwärtige Quinte (Fünf) in der Musik genau unserer Fingerzahl entspricht???